Implicants

Motivation: Implicants §

• Finding implicants allow us to find the lowest-cost implementation

Definitions: Implicants §

• Literal: Each appearance of a variable - complemented or uncomplemented - is called a literal
  • E.g. $x_1{x}_2^{\prime }$ has 2 literals
• Implicant: If function $f$ takes value 1 whenever product term is $1$, so that $p$ “implies” $f$, then $p$ is an implicant of $f$
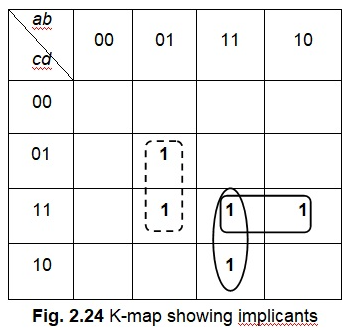
• Prime Implicant: An implicant is a prime implicant which forms the largest group possible to cover 1s
  • In the below image, there are 4 prime implicants. If a group has not been circled, the cells it’s covering can already be covered by a larger group
  • 
• Cover: A cover is a set of implicants which account for all valuations (?) for which a given function $f=1$
  • Different sets of coverts exist for most functions
    • E.g. The set of minterms for which $f=1$ is a cover
    • E.g. The set of prime implicants is a cover
  • For the example function given below, valid covers include
    • $C=\{m_5,m_7,m_{11},m_{14},m_{15}\}$
    • $C=\{a^{\prime }bd,abc,acd\}$
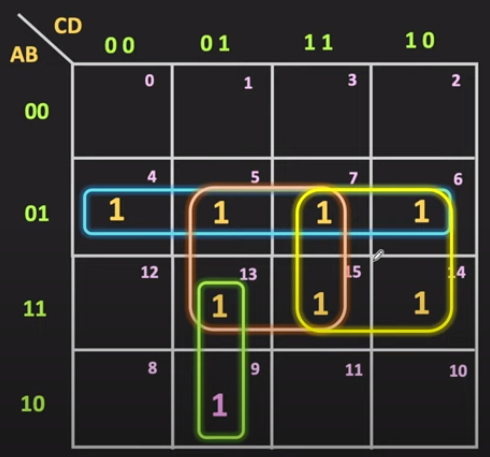
• Essential Prime Implicant: Essential Prime Implicants are prime implicants which cover an output value 1 that no combination of other prime implicants can cover
  • In the example below, $abd$ is an essential prime implicant, as it is the only prime implicant that covers $m_5,m_7$
• Cost: Number of gates + Number of inputs to all gates
  • Note that complemented input variables/literals are always available free ot charge. However, NOT gates will cost extra

Example: Implicants

The k-map below is the SOP implementation of the function $f(a,b,c,d)=abd+abc+acd.$

Note that $abd$ is a prime implicant; if we were to remove variable $a$, the remaining term $bd$ would form a 2x2 square in the centre of the k-map. This square would include the minterm $m_{1}3$, which has a value of 0, and thus $bd$ does not imply $f$.

Procedure: Minimisation §

The procedure for creating a minimal-cost function is the following:

1. Find all prime implicants (largest grouping possible covering 1s) for $f$
2. Find essential prime implicants (has “exclusive” access to a minterm) for $f$
3. If the set of essential prime implicants cover all cells for which $f=1$, this SOP set is the minimal-cost cover for $f$. If there are still “straggler” $f=1$ cells which are not covered, find the largest non-essential prime implicants that can be added to complete the cover

Example: Minimisation